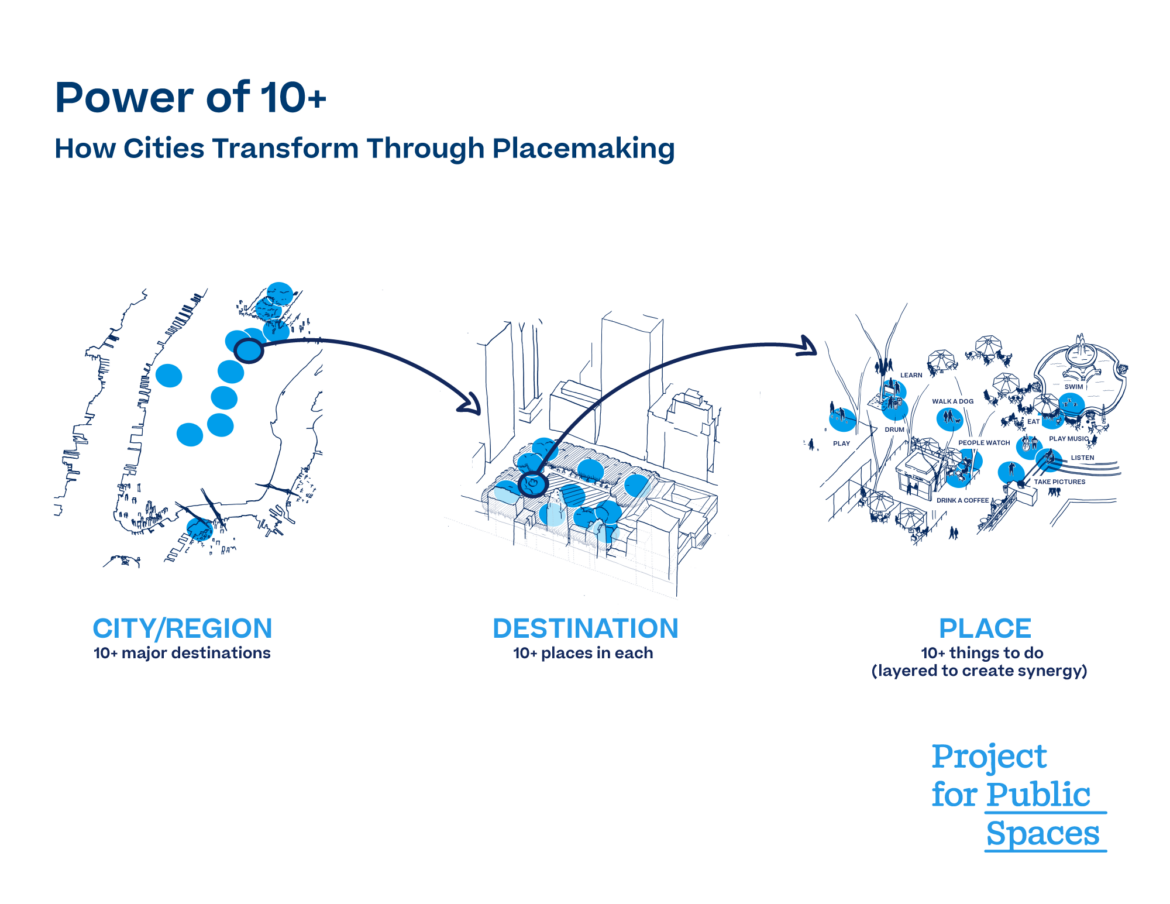
Introduction
The concept of the ‘Power of 10’ is fundamental in mathematics, significantly influencing various fields such as science, engineering, and finance. Understanding this mathematical principle allows for easier computations and a deeper grasp of exponential growth or decay. The notation has great importance, especially in scientific notation, where very large or very small numbers can be expressed succinctly and clearly.
The Basics of Power of 10
In mathematics, expressing a number as a Power of 10 means using the base 10 raised to an exponent. For example, 102 equals 100, indicating that 10 is multiplied by itself two times. Similarly, 10-1 equals 0.1, or simply 1 divided by 10, showcasing the utility of Powers of 10 beyond just large numbers.
Applications Across Disciplines
The Power of 10 is especially vivid in scientific applications. For instance, in chemistry, the concentration of solutions is often indicated using Molarity which might demand expressions like 1.0 × 10-3 M (molar). In the field of astronomy, distances are frequently represented using Powers of 10 due to the incredible scale involved; the distance to the nearest star outside our solar system is approximately 4.24 × 1013 km.
In computing, Powers of 10 play a crucial role in representing data sizes, where a kilobyte is 103 bytes and a megabyte is 106 bytes. This consistent approach helps in understanding data storage and transmission.
Visualising Powers of 10
Visual representations, such as logarithmic scales, can make comprehension easier, translating enormous values into manageable formats. The Power of 10 is not just about quantifying numbers; it’s about unveiling relationships between different magnitudes, from microscopic elements to celestial bodies.
Conclusion
The Power of 10 serves as a vital tool, enabling students, scientists, and professionals across various disciplines to express and manipulate numbers efficiently. Understanding its applications not only fosters mathematical proficiency but also enhances analytical skills in interpreting scientific data. As we continue to evolve technologically and scientifically, mastering the Power of 10 remains crucial in fostering clearer communication of numerical information.